Introduction
A genetic algorithm (GA) is an evolutionary algorithm, which is inspired by Charles Darwin’s theory of natural evolution. Genetic algorithms are commonly used to solve optimization problems and search problems with operators such as mutation, crossover and selection, which are inspired by biological evolution mechanisms.
Gene algorithm is usually realized by a computer simulation. For an optimization problem, a certain number of candidate solutions (called "individuals") can be abstractly represented as chromosomes, so that the population can evolve to a better solution. Traditionally, a chromosome (later to becoming a solution) is represented by binary numbers (i.e., a string of 0 and 1), but other representation methods can also be used. Evolution starts with a population of completely random individuals, and then occurs generation after generation. In each generation, the fitness of the entire population is evaluated, multiple individuals are selected from the current population based on their fitness, and a new life population is generated through natural selection and mutation. The new population becomes the current population in the next iteration of the algorithm.
基因演算法(GA)是一種進化演算法,其靈感來自查爾斯·達爾文(Charles Darwin)的自然進化理論。 基因演算法通常用於解決最佳化問題和搜尋問題,最初是受到進化生物學中的一些現象的啟發而發展起來的,包括突變、交配以及自然選擇等等。
基因演算法通常透過電腦模擬來實現。對於一個最佳化問題,一定數量的候選解(稱為個體)可視為染色體,使種群進化成為更好的解。慣例上,染色體(也就是後來的解)用二進位數字表示(即0和1的序列),但也可以用其他表示方法。從完全隨機個體的種群開始,之後一代一代的演化。在每一代中評價整個種群的適應度,從當前種群中由它們的適應度選擇一定數量的個體,通過自然選擇和突變產生新的生命種群,而成為演算法的下一次迭代中的種群。
Genetic Algorithm
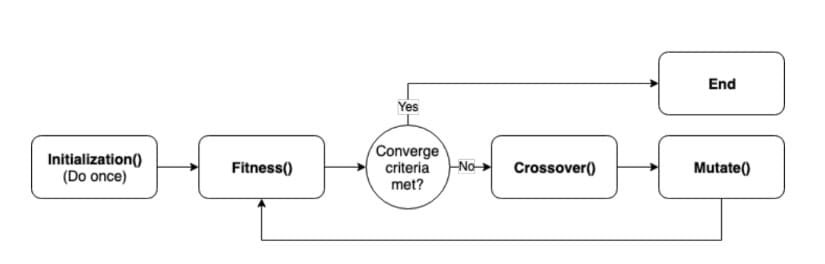
GA can generally be divided into six steps: initialization, selection, crossover, mutation, convergence, and termination. First, a number of genes are randomly initialized as the first generation. A gene is in fact a series of 0's and 1's. During each successive generation, a (high-quality) portion of the existing population is selected to breed a new generation with operators such as crossover and mutation. Convergence criteria are then checked whether they are met. The four steps in the middle cycle until the convergence criterion is met. Finally, the algorithm terminates, and the optimal solutions are found.
GA一般可分為六個步驟:初始化,選擇,交配,變異,收斂和終止。 第一步,隨機初始化一些基因當作第一代。 基因實際上是由0和1所組成的數字序列。 在每個連續的世代中,選擇現有種群高分數的基因,使用其來進行交配和突變來培育新一代。 然後檢查新的子代是否滿足收斂標準。 直到達收斂標準為止,中間的四個步驟會一直循環。 最後,演算法停止,找到最佳解。
Introduction to proper nouns
- Individual: The solution of the optimization problem, expressed as a sequence of 01 variables, called gene. Such as: 0101111010.
- Population: Composed of several individuals, the size of the population has a great influence on the quality of the genetic algorithm.
- Generation: The first generation is randomly initialized, and the next generation population is generated through crossover and mutation.
- 個體:最佳化問題的解,表示為一個01變數序列,稱之為基因。如:0101111010。
- 種群:由數個個體所組成,種群的大小對基因演算法的好壞影響很大。
- 世代:隨機初始化產生第一代種群,經過交配和突變產生下一代種群。
Steps of GA
- Initialization: The process of setting the population size (n) and randomly generating individual genes, such as: 1: 0101111010, 2: 1011010000,..., n: 0111101001.
- Fitness: It is used to Judge the performance of genes. The judgment standard is determined by the user. Genes are usually evaluated with a score called fitness.
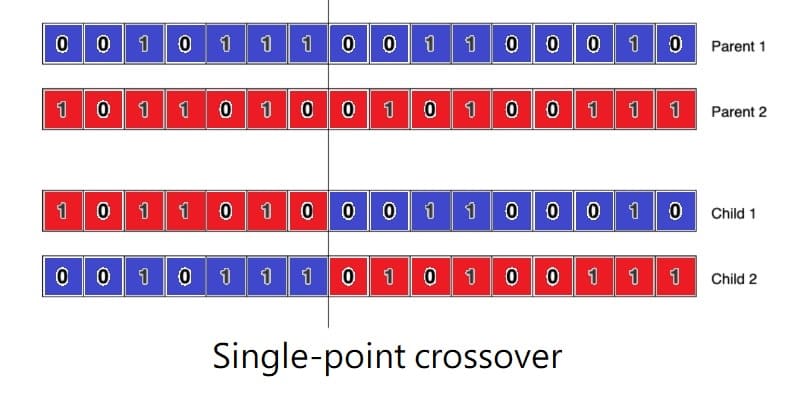
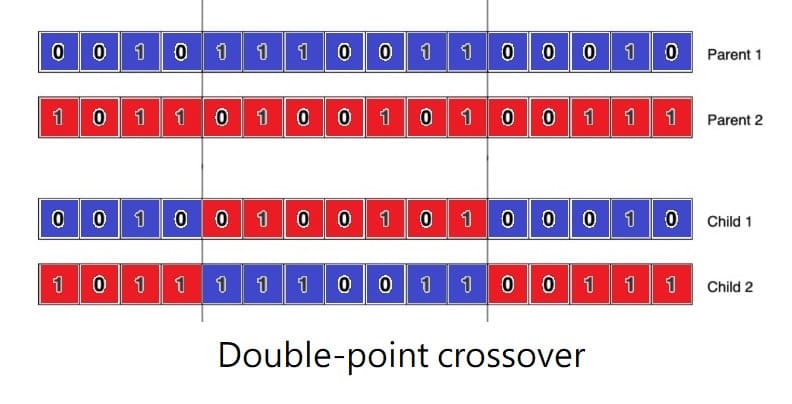
- Crossover: Mix parent genes to become genes of new generation. This process are divided into single-point crossover and double-point crossover, where crossover points are randomly selected.
- Single-point crossover: Choose one crossover point to mix two genes to generate a new gene.
- Double-point crossover: Choose two crossover points to mix two genes to generate a new gene.
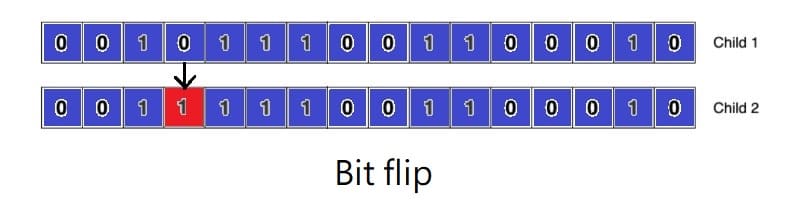
- Mutation: Simulate the genetic mutation of biology, increase complexity, and avoid premature convergence and not reach the optimal solution. Usually divided into bit flip and inversion.
- Bit-flip: Select a bit to flip its 01. The original 0 will change to 1, and the original 1 will change to 0.
- Reversal: Swap the 0 and 1 of the entire gene.
-
Convergence Criteria: Conditions for termination, usually divided into two types:
- The score (fitness) meets the condition: the algorithm terminates if the score of genes has reached the requirement.
- N times iterations: After enough iterations of generations to evolve, the algorithm terminates. If N is not reached, continue to iterate and evolve.
- 初始化:設定種群大小(n),隨機產生個體基因的過程,如:1: 0101111010、2: 1011010000、…、n: 0111101001。
- 適應度函式:用來評斷基因的表現,判斷標準是由使用者決定,通常會給基因評比一個分數,稱為適應度。
- 交配:以父母基因混和成為新的子代基因,隨機產生交配點,又分為單點交配和雙點交配。
- 單點交配:選擇一個交配點將兩條基因混和產生新的基因。
- 雙點交配:選擇兩個交配點將兩條基因混和產生新的基因。
- 突變:模擬生物學的基因變異,增加複雜度,避免過早收斂而未達到最佳解,分為位元翻轉和反置。
- 位元翻轉:選擇一個位元將其01翻轉,原本0則變1,原本1則變0。
- 反置:將整條基因的0和1互換。
-
收斂標準:停止演化的條件,通常分為兩種:
- 分數(適應度)達到條件:子代的分數已達到要求即可停止
- 經過 N 個世代:經過夠多次世代演化即可停止,若還沒達到則繼續繁殖演化。
Parameters
- Population size (P): the number of chromosomal individuals in the population.
- String length (l): The length of the chromosome in the individual.
- Mutation probability (pm): the probability of mutation, usually 0.1 or less.
- Convergence criteria: conditions for terminating the algorithm.
- 種群規模(P):即種群中染色體個體的數目。
- 字串長度(l):個體中染色體的長度。
- 突變概率(pm):突變發生的機率,通常為0.1或更小。
- 收斂條件:終止演算法的條件。
Application
There are many problems to which it is impossible to find the optimal solution within a limited time, such as the scheduling problem and many practical engineering problems. There is a classic traveling salesman problem (TSP) asking the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" Note that finding the shortest route is an optimization problem. Assuming there are only 26 [n] cities, there are 25! [(N-1)!], about 1.55 * 10 ^ 25 different routes, and the calculation takes 500 billion years. Regarding this kind of problem, we can only compromise and find an approximate solution. The genetic algorithm is very suitable for solving this kind of problem. It can quickly find a good (although not optimal) solution even in a very complex solution space. The genetic algorithm allows the use of very complex fitness functions, and the range of variables (solutions) can be limited.
世界上有許多問題,在有限的時間內是無法找到最佳解的,例如,時間表安排問題,和許多實際工程問題。其中有一個很經典的旅行推銷員問題,給定一系列城市和每對城市之間的距離,求解推銷員必須到每一座城市恰好一次並回到起始城市的最短路徑(最佳化問題)。假設僅僅有26 [n]個城市,則有25! [(n-1)!],約 1.55 * 10 ^ 25 種不同的路徑,計算需耗時五千億年。關於這種問題,我們只能退而求其次找一個近似解,而基因演算法非常適合解決這種問題。基因演算法即使是在很複雜的解空間中,也能很快就能找到良好(並非最佳)的解,而且基因演算法允許使用非常複雜的適應度函式,並對變數(解)的變化範圍可以加以限制。
Real Instance
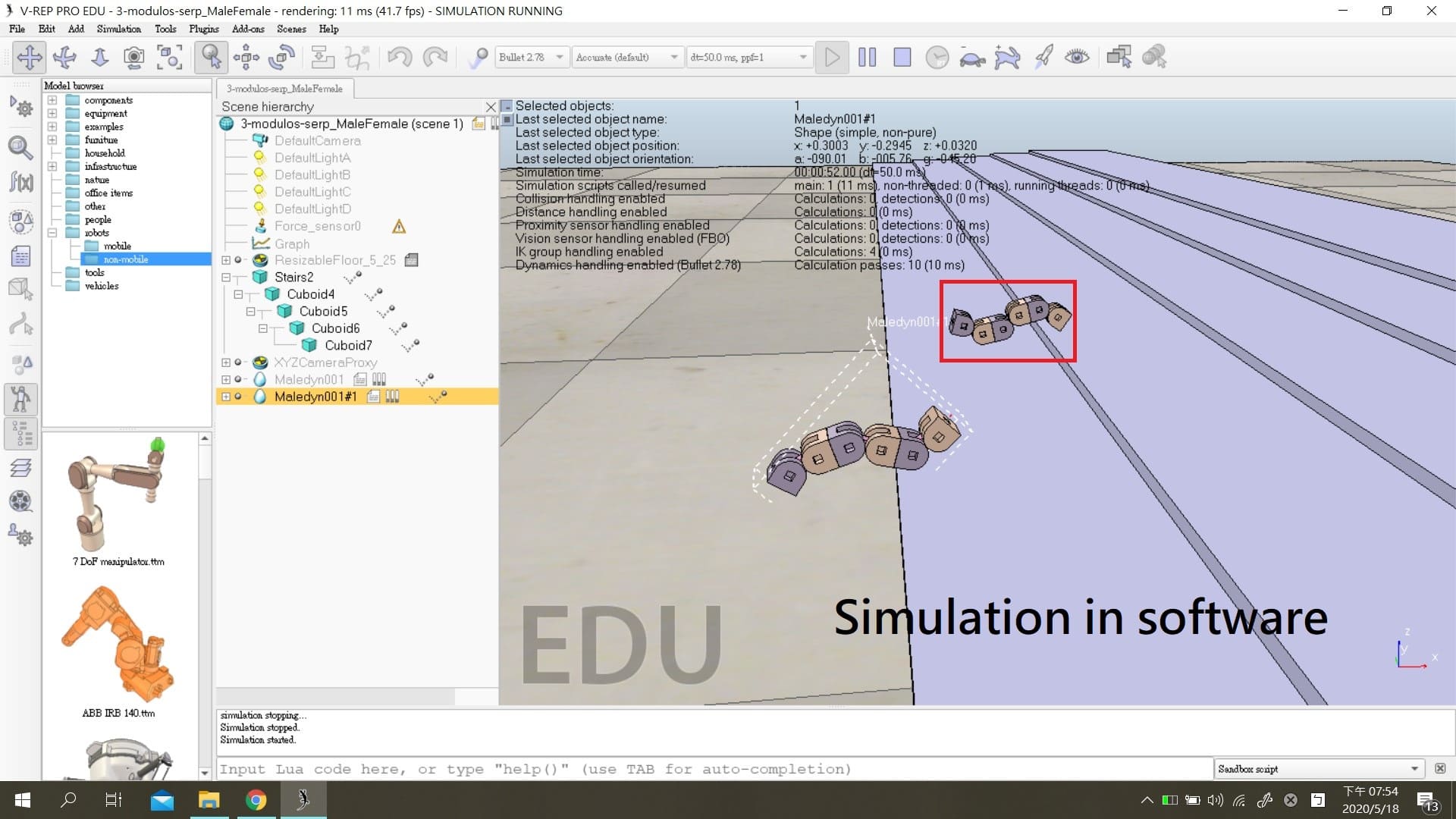
During my junior year in college, I participated in an independent research project with my peers to pursue genetic algorithms and control system. We worked with Prof. WeiYu Chiu to develop a modular reconfigurable robot for locomotion control. The modular robot has different modes for crawling and climbing, and the motor amplitude and phase (you can think of them as speed and angle) for each mode is calculated with genetic algorithm. We parse the gene as binary number and convert them to decimals for use. In the first generation of random genes, modular robots did not look like they were operating normally, and some even crawled backwards. When it evolves to the 20th generation, some modular robots can crawl normally. After we adjust some parameters, some modular robots can climb stairs.
在大學三年級時,我與幾個同學一起實作基因演算法和控制系統的專題。 我們與邱偉育教授開發了用於運動控制的可重組模組機器人。模組機器人有的爬行和爬樓梯模式,每種模式的馬達振幅和相位(可將它們視為速度和角度)都是使用基因演算法計算出來的。 我們將基因當作二進位的數,並將其轉換為十進位數以作為振幅和相位使用。在第一代隨機的基因的時候,模組機器人看起來完全不像是正常運作,甚至有些是往後爬的。當演化到第二十代的時候,有些模組機器人已可以正常爬行,我們調整一些參數之後,有些模組機器人就可以爬上樓梯。